GONI

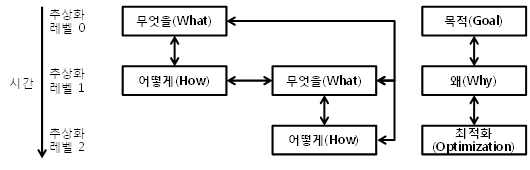
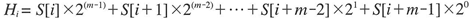TCP/IP 개요 TCP/IP 프로토콜 구조 인터넷을 통해 통신을 수행하는 개체는 크게 종단 시스템과 라우터로 나눌 수 있다. 종단 시스템(end-system)은 최종 사용자(end-user)를 위한 애플리케이션을 수행하는 주체가 되며, 인터넷에 연결된 PC, 워크스테이션, PDA, 휴대폰 등이 여기에 속한다. 라우터(router)는 종단 시스템이 속한 네트워크와 다른 네트워크를 연결함으로써 서로 다른 네트워크에 속한 종단 시스템끼리 상호 데이터를 교환할 수 있도록 하는 장비다. 종단 시스템과 라우터간, 라우터와 라우터간, 그리고 종단 시스템과 종단 시스템간 통신을 수행하기 위해서는 정해진 절차와 방법을 따라야 하는데 이를 프로토콜(protocol)이라 부른다. 1~4는 모두 상호 약속한 프로토콜을 이용..

Part1. 준비 학습 : 소켓 프로그래밍 입문 Chapter01 네트워크와 소켓 프로그래밍 TCP/IP 개요 TCP/IP 프로토콜 구조 패킷 전송 원리 IP 주소, 포트 번호 클라이언트/서버 모델 소켓의 개념 데이터 타입 통신 종단점 네트워크 프로그래밍 인터페이스 윈도우 소켓 특징 구조 윈속 어플리케이션 맛보기 Chapter02 윈도우 소켓 시작하기 오류 처리 윈속 초기화와 종료 소켓 생성과 닫기 소켓 생성 소켓 닫기 Chapter03 소켓 주소 구조체 다루기 소켓 주소 구조체 정의 바이트 정렬 함수 IP 주소 변환 함수 도메인 이름 시스템과 이름 변환 함수 Part2. 기본 학습 : 소켓 프로그래밍 기본 Chapter04 TCP 서버/클라이언트 TCP 서버/클라이언트 구조 동작 원리 [실습] 간단한 ..

제품군(Product Family) 제품 여러 개가 있고, 각 제품들은 또 다시 여러 종류로 나뉠 때 같은 종류의 제품들을 모아 놓은 것 다양한 접근 방법 및 Abstract Factory 패턴 문제를 요약하면, 어떻게 하면 같은 제품군에 속한 제품들의 객체만을 생성해서 사용하도록 명확히 보장받을 수 있는 가 하는 것 기본적인 방법 : 조건 비교 방식 if ( HP == 0 ) { //< HP용 객체 생성 } else if ( SUN == 0 ) { //< SUN 용 객체 생성 } else { //< 지원하지 않는 시스템 환경 } 프로그램 곳곳에 조건 비교 문장이 존재하게 됨 새로운 조건을 추가할 일이 발생하면 프로그램 전체를 찾아서 일일이 수정해야 함 좀 더 나은 방법 : 객체 생성 전담 클래스 활용 ..

CHAPTER 1. 소프트웨어 개발과 WHAT-WHY-HOW 생각 모델 소프트웨어 개발 원하는 목적(Goal)을 달성하기 위해 기준이 되는 개념이나 철학(Paradigm)을 바탕으로 특정한 과정(Process)을 거쳐 소프트웨어적인 해결책(Solution)을 만들어내는 것 소프트웨어 개발 개념 또는 철학 크게 구조적(Structured), 객체지향적(Object Oriented)으로 나뉨 비교항목 구조적 (Structured) 객체지향적 (Object Oriented) 주요 관점 기능(Function 또는 Process) 위주 데이터(Data) 위주 접근 방법 하향식 (Top Down) 분할 정복 (Divide and Qonquer) 상향식 (Bottom Up) 상호 관계 정의 산출물 구조 트리(Tree..

PART 1. 소프트웨어 개발과 디자인 패턴 CHAPTER 1. 소프트웨어 개발과 WHAT-WHY-HOW 생각 모델 소프트웨어 개발 기준 개념 또는 철학 소프트웨어 개발 과정 최적의 해결책 WHAT-WHY-HOW 생각 모델 CHAPTER 2. 소프트웨어 설계 및 디자인 패턴 소프트웨어 설계 좋은 소프트웨어 설계의 특성 좋은 소프트웨어를 설계하기 위한 도구 디자인 패턴의 정의 및 유용성 디자인 패턴 이해와 활용을 위한 이 책의 접근 방법 PART 2. 객체 생성을 위한 디자인 패턴 CHAPTER 3. 제품군별 객체 생성 문제 : ABSTRACT FACTORY 패턴 문제 사례 설명 다양한 접근 방법 및 ABSTRACT FACTORY 패턴 기본적인 방법: 조건 비교 방식 좀더 나은 방법: 객체 생성 전담 클래..

고지식한 검색 본문(Text) : 탐색 대상이 되는 문자열 패턴(Pattern) : 검색어(검색해야할 문자열) 이동(Shift) : 본문에서의 탐색 위치를 옮기는 것 고지식하거나 미련하거나 본문이 'ABCABACDC'라고 하고, 패턴은 'BA'라고 할 때 간단하게 생각해본다면 대부분 순차 검색을 통해 첫 번째 글자를 먼저 같은지를 검색하고 같은 것을 찾았을 때 뒤에 있는 2번째 글자를 검색할 것이다. 이 알고리즘은 마치 요령부지 않고 그저 우직하게 일하는 일꾼처럼 동작할 것이다. 이러한 알고리즘을 가리켜 고지식한 검색(Native Search), 또는 무식한 검색(Brute Force Search)라고 한다. 본문의 길이를 N, 패턴의 길이를 M이라고 했을 때, 본문 속에 존재하는 패턴을 찾기 위해 최악..

그래프를 소개합니다 오일러의 도구 "다리를 한 번씩만 건너 쾨니히스베르크의 모든 지역을 순회할 수 있을까?" 라는 문제를 해결하기 위해 오일러는 그래프를 고안해내고, 이를 도구로 이용하여 불가능함을 밝혀냈다. 오일러는 위의 그림을 좀 더 단순하게 만들어 각 육지를 정점(vertex)으로, 각 육지를 잇는 다리를 간선(edge)으로 표시했다. 이렇게 하면 쾨니히스베르크의 네 육지와 7개의 다리를 4개의 정점과 7개의 간선으로 나타낼 수 있다. 쾨니히스베르크의 다리 문제는 한붓그리기 문제가 됐다. 쾨니히스베르크의 그래프에서 정점 A,B,C,D 네 개는 모두가 홀수개의 선으로 연결되어 있기 때문에 한붓그리기가 불가능하고 따라서 7개의 다리를 한 번씩만 건너서 쾨니히스베르크의 모든 육지를 밟은 것을 불가능하다...

해시에 대하여 해시는 다양한 목적으로 사용될 수 있지만, 주로 다음과 같은 용도로 사용된다. 해시 테이블 : 해시테이블은 데이터의 해시 값을 테이블 내의 주소로 이용하는 궁극의 탐색 알고리즘이다. 빠르다고 정평이 나있는 이진 탐색보다도 빠르다. 암호화 : 해시는 입력받은 데이터를 완전히 새로운 모습의 데이터로 만든다. 해시를 통해 변환된 데이터는 원본의 모습을 알아볼 수 없을 정도로 완전히 달라진다. 이 특성 때문에 해시는 암호화 영역에서 아주 주요하게 사용되고 있다. SHA(Secure Hash Algorithm)알고리즘이 그 대표적인 예이다. 데이터 축약 : 해시는 길이가 서로 다른 입력 데이터에 대해 일정한 길이의 출력을 만들 수 있다. 이 특성을 이용하면 커다란 데이터를 '해시'하면 짧은 길이로 ..

우선순위 큐 먼저 들어간 요소가 먼저 나오는(First-In First Out)자료구조를 일컫어 '큐(Queue)'라고 한다. 우선순위 큐(Priority Queue)도 보통의 큐처럼 동작하지만 '우선순위' 속성을 갖는 데이터를 다룬다는 것이 다르다. 우선순위 큐의 삽입 연산 우선순위 큐의 삽입(Enqueue)은 요소의 우선순위 오름차순으로 연결된다. 새로운 요소가 삽입될 때 우선순위를 비교하여 새로운 요소가 들어가야할 자리에 삽입된다. 우선순위 큐의 제거 연산 우선순위 큐의 제거(Dequeue) 연산은 전단만 제거하면 된다. 우선순위 큐의 구현 다음에 나오는 힙을 배우고 구현 힙 여기서 말하는 힙은 프로그래밍에서 말하는 자유저장소(Free Store)가 아니라, 힙 순서 속성(Heap Order Pro..

데이터를 찾아서 컴퓨터에서의 탐색이란 '데이터'를 찾는다라는 의미 각각의 자료구조(배열,링크드리스트,트리 등등)에서 탐색의 방법이 다를 수 있다 순차 탐색 순차 탐색(Sequential Search)은 데이터 집합의 처음부터 끝까지 차례대로 모든 요소를 비교해서 데이터를 찾는 탐색 알고리즘이다. 정렬되어 있지 않은 데이터 집합에서 원하는 데이터를 찾을 수 있는 유일한 방법이고 구현이 간단해 버그를 만들 가능성이 적다는 장점이 있다. 자기 구성 순차 탐색 자주 사용되는 항목을 데이터 집합의 앞쪽에 배치함으로써 순차 탐색의 검색 효율을 끌어올리는 방법이다. 자주 사용되는 항목을 어떻게 선별하는가에 따라 세 가지 방법으로 나뉜다. 전진 이동법(Move To Front) 전진 이동법은 어느 항목이 한 번 탐색되..